
This describes a horizontal asymptote A horizontal line to which a graph becomes infinitely close where the x-values tend toward ±∞.
#Graph a piecewise function how to#
We will learn how to identify Symmetry given a graph and also how to determine whether a function is symmetric using algebraic techniques. In other words, as the x-values become very large the resulting y-values tend toward zero. There are countless types of symmetry, but the ones we want to focus on are.

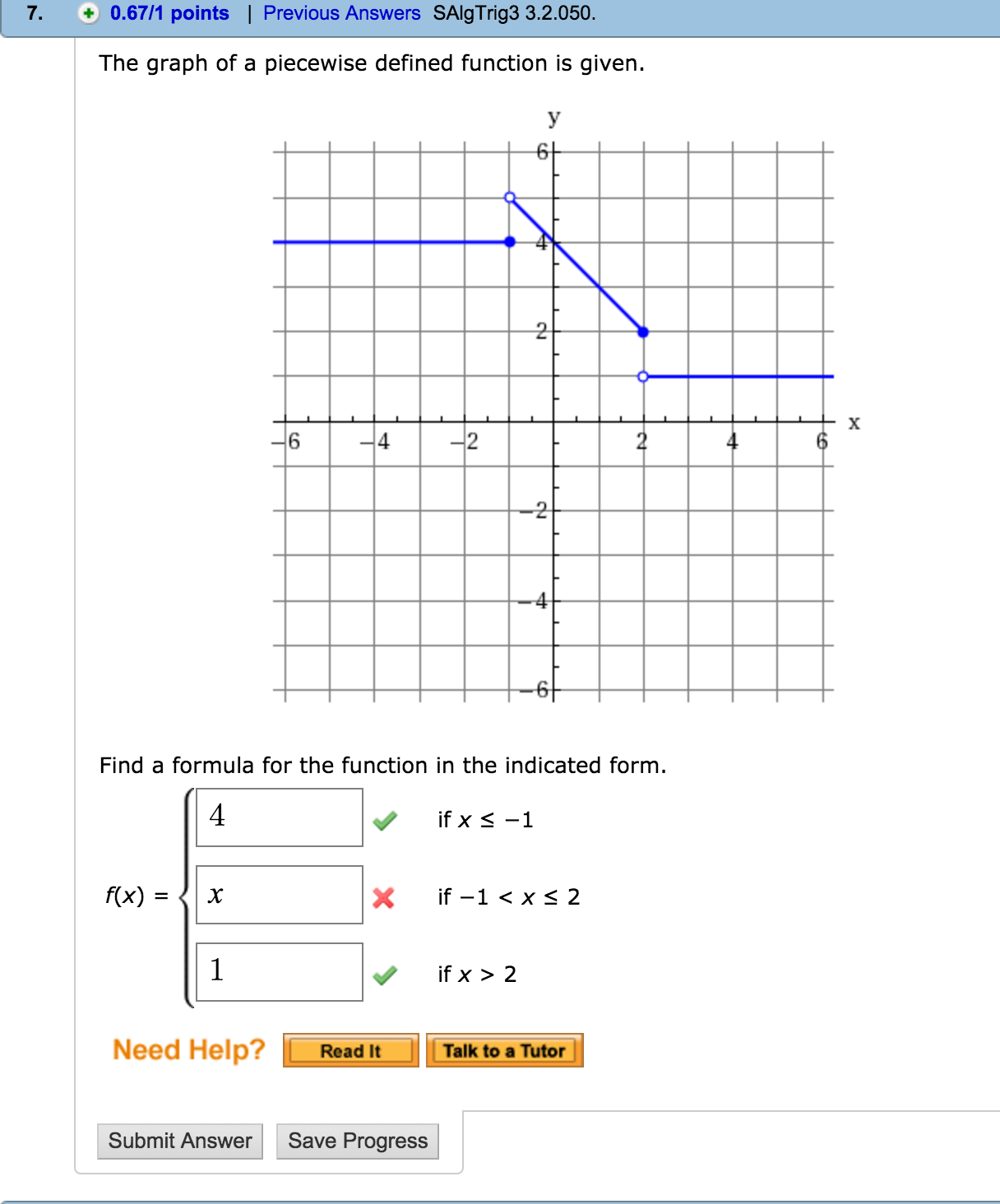
Furthermore, where the x-values are very large the result of the reciprocal function is very small.į ( 10 ) = 1 10 = 0.1 f ( 100 ) = 1 100 = 0.01 f ( 1000 ) = 1 1,000 = 0.001 Evaluate equations by nding the domain in which the x falls. Evaluate on a graph by nding the x on the x-axis, move vertically until you hit the function, write the point, and the y-coordinate is the value of the function at x. This describes a vertical asymptote A vertical line to which a graph becomes infinitely close. Piecewise functions are several different functions grouped for specic domains. In other words, as the x-values approach zero their reciprocals will tend toward either positive or negative infinity. Sometimes, we come across a function that requires more than one formula in order to obtain the given output. The reciprocal of an x-value very close to zero is very large. , defined by f ( x ) = 1 x, is a rational function with one restriction on the domain, namely x ≠ 0.

Bring it all together, and you have your graph This tutorial shows you the entire process for graphing a piecewise linear function. The reciprocal function The function defined by f ( x ) = 1 x. If you want to graph a piecewise linear function, graph each function on it's specific interval separately. The domain and range both consist of real numbers greater than or equal to zero [ 0, ∞ ).


 0 kommentar(er)
0 kommentar(er)
